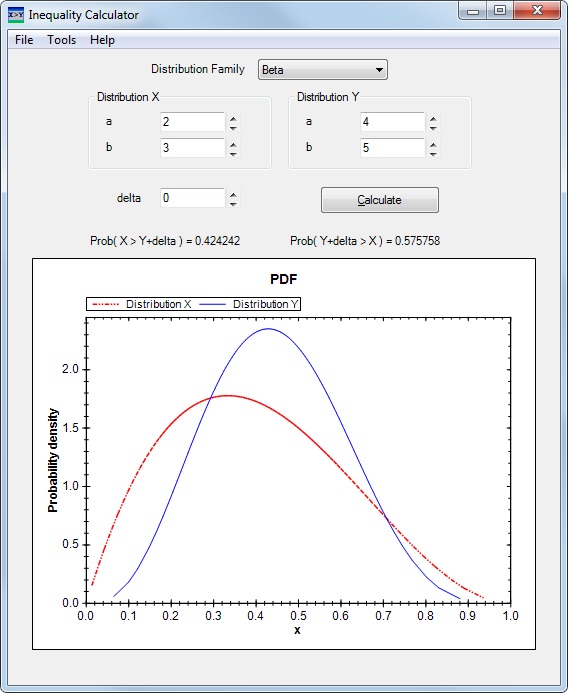
Inequality Calculator

Given two random variables X and Y, this application calculates P(X > Y + δ) and produces graphs of the densities of the two random variables. The supported distribution families are

• Beta
• Gamma
• Inverse Gamma
• Log normal
• Normal
• Weibull

What's New in Version 3.2.0

• Now uses Microsoft .NET Framework 4.8.1
• Other updates and improvements

Requirements

• Windows 11
  (other Windows versions may be compatible but this has not been tested)
• Administrative permissions may be required to install Inequality Calculator depending on the chosen installation location.
• The following packages will be installed if they are not present:
  • Microsoft .NET Framework 4.8.1
  • Microsoft Visual C++ 14 x86 runtime redistributable library
• To view the the Inequality Calculator user's guide a PDF file viewer (not included with the software) such as Adobe Reader (available for free here) must be installed.
• To follow the "Send feedback via email" link in the Help -> About window, an email client such as Microsoft Outlook (not included with the software) must be installed.

For more information, see the Inequality Calculator user's guide included with the download distribution.

This software is included as a utility inside Adaptive Randomization, Predictive Probabilities, and Multc Lean.

J. Kyle Wathen and Hoang Q. Nguyen developed the original user interface using Microsoft's C# in Visual Studio .

Clift Norris, John Venier, and Ren Zheng updated the software, fixed bugs, and provided other enhancements.

John Cook implemented the numerical algorithms using Visual C++. Technical reports are available for numerical algorithms [1] and analytical results [2] related to the Inequality Calculator.