Introduction

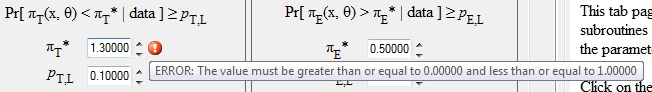
This computer program provides a basis for constructing and simulating the EffTox phase I-II clinical trial design described in the paper “Dose-finding based on efficacy-toxicity trade-offs”, Thall and Cook, Biometrics 60:684-693,2004. Please read this paper before using this program, which implements the trial design and simulation. Please note that very important improvements/refinements have been made in two key elements, (1) the prior and (2) the trade-off contour. These are explained below.

Input

The input required to specify a design and run computer simulations is as follows.

Notation: Given raw doses d₁, . . . , d_J, the standardized doses x₁, . . . , x_J, used in the model are defined as follows: l_j = log(d_j), and x_j = l_j - ( l₁ + . . . + l_J )/J. Denote  π_E(x) = Pr(Efficacy at dose x),  π_T(x) = Pr(Toxicity at dose x). Suppressing dose, a marginal probability pair is π = (π_E, π_T).

N = Maximum sample size

c = Cohort Size

The number of doses to be studied, their units, and their numerical values in those units.

The starting dose for the first cohort.

The prior on the model parameters, specified initially in terms of elicited prior means of π_T(x) and π_E(x) at each x.

Three fixed, equally desirable probability pairs π₁*, π₂*, π₃* needed to construct the target efficacy-toxicity trade-off contour.

A fixed upper limit π_T* on π_T(x), and an accompanying lower probability decision threshold p_T,L.

A fixed lower limit π_E* on π_E(x), and an accompanying lower probability decision threshold p_E,L.

Several simulation scenarios, each consisting of fixed assumed true values π_E(x), π_T(x) for each x.

Important Guidelines for Calibrating EffTox Design Parameters

Efficacy-Toxicity Trade-off Contour

The EffTox method is very sensitive to the efficacy-toxicity trade-off contour, C. Avoid using C that rises quickly and then becomes relatively flat, or that is not reasonably steep. For higher dose levels, such C gives a small trade-off-based payoff for large increases in π_E(x) when there is a small increase in π_T(x), with the very undesirable consequence that the resulting design is unlikely to escalate to truly desirable higher doses with higher π_E(x) and acceptably low π_T(x). To avoid this undesirable behavior, always use a contour that is sufficiently steep. Although the contour is based, initially, on the three pairs π₁*, π₂*, π₃* elicited from the physician, you must adjust the contour as needed, and explain this to the physician, since it is not intuitively obvious why their initial contour may in fact produce pathological, undesirable behavior.

Prior Calibration

The EffTox method is very sensitive to the numerical prior hyper-parameter values, so it is essential to calibrate the hyper-parameters. Begin by inputing elicited values of mean {π_E(x)} and mean {π_T(x)} at each dose x, and your desired target mean prior Effective Sample Size (ESS). The EffTox program will solve for the hyper-means and standard deviations (SDs) based on these values. The target mean ESS value should not be either too large (which may produce an overly informative prior that the data may not be able to overcome) or too small (which may produce a pathological prior with induced priors for π_E(x) and π_T(x) that have too much mass near 0 and 1). Prior ESS values that work well range between roughly 0.5 and 1.5, with values of about 0.90 often working well. The prior ESSs, which have numerical values with a simple intuitive interpretation, determine the prior SDs, whose numerical values have no intuitive meaning.

Calibrating Design Parameters by Simulation

It is essential to simulate your design under several dose-outcome scenarios, and use repeated simulations as a basis for calibrating your design parameters and prior hyperparameters, to make sure that the design has good operating characteristics (OCs), before including the design in an actual clinical trial protocol. Specify a reasonable set of possible dose-outcome scenarios in terms of fixed values of {π_E(x), π_T(x)}. The aim is to obtain a design with good OCs. Make sure to include scenarios where:

1. the “best” dose is low in the dose domain
2. the “best” dose is near the middle of the dose domain,
3. the “best” dose is high in the dose domain
4. due to excessively high toxicity, no dose is acceptable, and
5. due to excessively low efficacy, no dose is acceptable.

Do preliminary simulations to calibrate the prior and design parameters. You may use 100 to 400 repetitions at this stage to speed up this process. Sensitivity to ESS, C, cohort size, N, and the lower probability thresholds may be assessed by varying each of these parameters one at a time. When you have obtained a final design with good OCs, do a final simulation of all scenarios with 1000 or 2000 repetitions. Include a tabulation of the OCs, along with all numerical prior and design parameters, in the Statistical Methods section of the clinical trial protocol.

Troubleshooting

The EffTox program has a number of validation rules built in to reduce the likelihood of error. The general method for indicating a violation of a validation rule is a flashing icon, a red dot with a white exclamation point inside. Placing the mouse over the validation icon produces a tool tip which indicates the rule that has been violated. For example, the following shows the result of entering 1.3 in a box expecting a probability.

In addition to the flashing icon, the software will generally not let you go on to another field until the error is corrected: If you’re unable to go on to the next thing you want to do, look for a flashing red icon.

Illustrative Example

This example is from a trial in advanced prostate cancer. Five dose levels were studied, d = 1, 2, 4, 6.6, 10 mcL/kg. The prior marginal mean outcome probabilities for the 5 dose levels were (.20, .40, .60,.80, .90) for π_E(x) and (.02, .04, .06, .08, .10) for π_T(x). In the trial, N = 39 and c = 3, the first cohort was treated at d = 1, the upper limit on π_T(x) was π_T* = 0.30, the lower limit on π_E was π_E* = 0.50, and the acceptability criterion lower probability thresholds were p_T,L = p_E,L = 0.10.

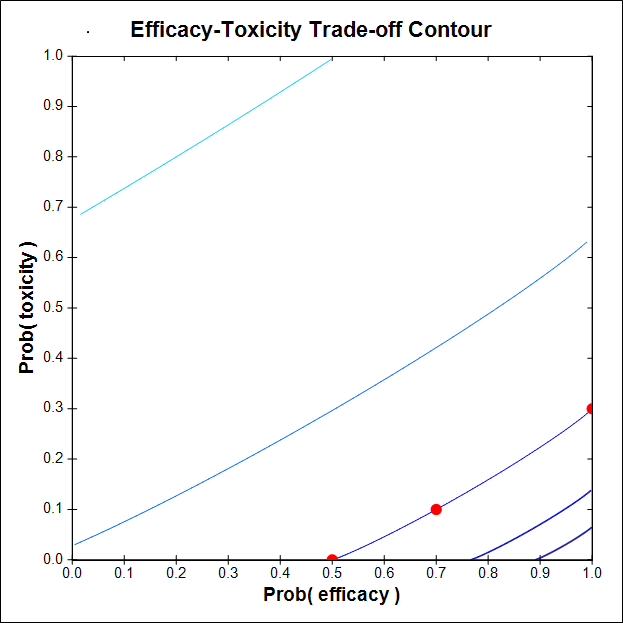
Initially this trial was designed using a contour C based on the three trade-off probability pairs (π_E, π_T) = (0.50, 0), (1, 0.30), (0.70, 0.10), that was too flat. This produced a pathological design that failed to escalate when higher x gave higher π_E(x) and acceptable π_T(x). The figure shows that C is not sufficiently steep.

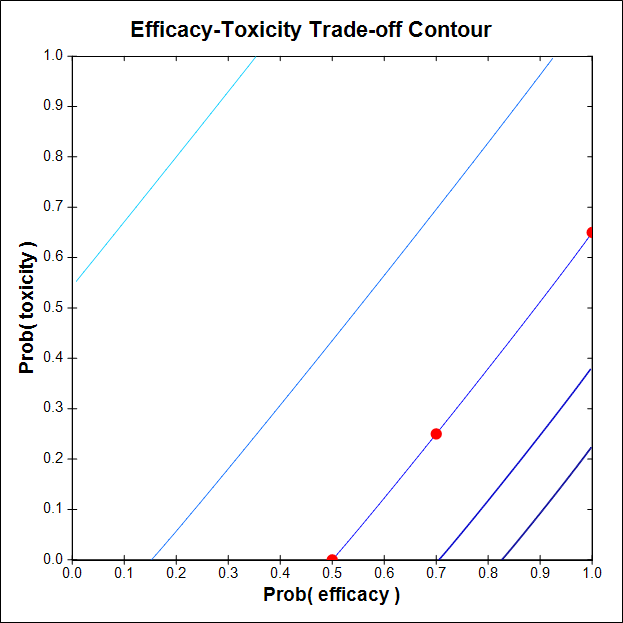
The corrected contour, which gave a much better design, was based on the three trade-off probability pairs (π_E, π_T) = (0.50, 0), (1, 0.65), (0.70, 0.25). The figure shows that this new C is sufficiently steep, so that the contour rewards exploring higher doses to get higher π_E(x) and when π_T(x) is acceptable.

The new design also used prior ESS = 0.91. This design has the OCs given in the table below. Note that:

1. Doses with values of true π_T(x) at or slightly above the upper limit 0.30 are reasonably safe but difficult to select.
2. Doses with values of true π_E (x) at or slightly below the lower limit 0.50 are reasonably efficacious but difficult to select.
3. It is extremely difficult to distinguish between adjacent doses for which the differences between π_E(x) or π_T(x) are 0.10 or smaller, which is true in any case, especially with N = 39 or smaller.

Operating Characteristics of the Design with N = 39

Sensitivity to N Under Scenario 2

The above design is reasonable for N = 39. However, it always is very useful to explore any design's sensitivity to N, to see what may be gained in the way of reliability with larger N. The following sensitivity analysis, in Scenario 2, illustrates how, for higher dose levels, both selection probability mass and numbers of patients treated are shifted to higher, more desirable doses as N is increased. Note that, under Scenario 2, the highest two dose levels have the highest trade-off values 0.28 and 0.33, but these are numerically very close and thus it is very difficult to distinguish between them. Similarly, on the probability domain, distinguishing between their respective toxicity probabilities 0.20 and 0.30, and their respective efficacy probabilities 0.80 and 0.90, also is very difficult. In practice, either of these two doses would be a good choice. The EffTox design gives selection percentages of the highest two dose levels, respectively, (28%, 33%) with sum = 61% for N = 39, (34%, 36%) with sum = 70% for N = 54, (31%, 38%) with sum = 69% for N = 69, and (31%, 42%) with sum = 73% for N = 84.